Trabajo y energía de la partícula
Una fuerza F realizará trabajo en una partícula sólo cuando ésta sufra un desplazamiento en la dirección de la fuerza.
Si la fuerza F hace que la partícula se mueva a lo largo de la trayectoria s de la posición r a una nueva posición r´, el desplazamiento es entonces dr=r´-r. La magnitud de dr es ds, la longitud del segmento diferencial a lo largo de la trayectoria. Si el ángulo entre las colas de dr y F es θ, entonces el trabajo realizado por F es una cantidad escalar, definida por:
dU = F ds cos θ
Por definición del producto punto esta ecuación también puede escribirse como:
dU = F dr
La unidad de trabajo en unidades SI es el joule (J) el cual es la cantidad de trabajo realizada por una fuerza de un newton cuando recorre una distancia de un metro en la dirección de la fuerza (1 J = 1 N * m).
En el sistema FPS, el trabajo se mide en unidades libra-pie (pie * libra), que es el trabajo realizado por una fuerza de una libra que actúa a lo largo de una distancia de un pie en la dirección de la fuerza.
Empleo de las ecuaciones del trabajo y la energía para la partícula.
Considere la partícula que aparece en la figura, localizada en la trayectoria definida con respecto a un sistema de coordenadas inerciales. Si la partícula tiene una masa m y se somete a un sistema de fuerzas externas, representado por la fuerza resultante FR=F, entonces la ecuación de movimiento de la partícula en la dirección tangencial es Ft=mat.
Si aplicamos la ecuación cinemática at=v dv/ds e integramos ambos lados y suponemos que inicialmente la partícula tiene una posición s=s1y una rapidez v=v1 y después s=s2 y v=v2, tenemos:
Figura
En la figura, observe que Ft=Fcos0 puesto que la ecuación anterior define el trabajo, el resultado final se escribe como:
Empleo de las ecuaciones del trabajo y la energía para partículas conectadas.
El principio de trabajo y energía puede ampliarse para incluir un sistema de partículas aisladas dentro de un espacio cerrado como se muestra en la figura. Aquí la partícula i-ésima arbitraria, de masa mi, está sometida a una fuerza externa resultante Fi y a una fuerza interna resultante fique todas las demás partículas ejercen en la partícula i-ésima. Si aplicamos el principio de trabajo y energía a ésta y a cada una de las demás partículas que componen el sistema, entonces, puesto que el trabajo y la energía son cantidades escalares, las ecuaciones se suman algebraicamente, lo que da
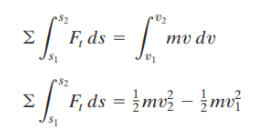

Comentarios
Publicar un comentario