La segunda parte de la cinemática rectilínea se llama movimiento curvilíneo y este ocurre cuando una partícula se desplaza a lo largo de una trayectoria curva. Como esta trayectoria a menudo se describe en tres dimensiones, utilizaremos análisis vectorial para formular la posición, aceleración y velocidad de una partícula. En esta sección se analizan los aspectos generales del movimiento curvilíneo y en secciones subsiguientes consideraremos tres tipos de sistemas de coordenadas que se usan con frecuencia para analizar este movimiento.
Posición
Considere una partícula situada en un punto de una curva espacial definida por la función de trayectoria s(t). El vector de posición r = r(t) designará la posición de la partícula, medida con respecto a un punto fijo O. Observe que tanto la magnitud como la dirección de este vector cambiarán a medida que la partícula se mueve a lo largo de la curva.
 |
| Figura 1 |
Desplazamiento
Suponga que durante un breve intervalo 𝚫t la partícula se mueve una distancia 𝚫s a lo largo de la curva a una nueva posición, definida por r' = r + 𝚫r. El desplazamiento 𝚫r representa el cambio de posición de la partícula y se determina mediante una resta vectorial, es decir 𝚫r = r' - r |
| Figura 2 |
Velocidad
Durante el tiempo 𝚫t, la velocidad promedio de la partícula es: |
| Figura 3 |
La velocidad instantánea se determina con esta ecuación cuando 𝚫t➡️0, y por consiguiente la dirección de 𝚫r tiende la tangente a la curva. por consiguiente,
 |
| Figura 4 |
Como dr sera tangente a la curva, la dirección de v también es tangente a la curva,
 |
| Figura 5 |
La magnitud de v, conocida como la rapidez, se obtiene al tener en cuenta que la longitud del segmento de línea recta 𝚫r en la figura 2 tiende la longitud del arco 𝚫s a medida que 𝚫t➡️0, tenemos que
Por tanto, la rapidez se obtiene al diferenciar la función de la trayectoria s con respecto al tiempo.
 |
| Figura 6 |
Aceleración
Si la velocidad de la partícula es v en el instante t y v' = v + 𝚫v en el instante t + 𝚫t, entonces la aceleración promedio de la partícula durante el intervalo 𝚫t es
 | |
| Figura 7 |
Donde 𝚫v = v' - v. Para estudiar la tasa de cambio en el tiempo, los dos vectores de velocidad en la figura 7 se trazane en la figura 8 de modo que sus colas queden el punto fijo O' y sus cabezas de punta de flecha toquen puntos situados en la curva. Esta curva se llama hodógrafa y cuando se construye, describe el lugar geométrico de puntos para la cabeza de punta de flecha del vector de velocidad, del mismo modo en que la trayectoria s describe el lugar geométrico de puntos para la cabeza de punta de flecha del vector de posición. Para obtener la aceleración instantánea, hacemos que 𝚫t➡️0 en la ecuación anterior. En el límite 𝚫v tenderá la tangente a la hodógrafa y por tanto
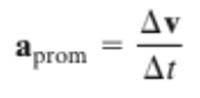

Comentarios
Publicar un comentario